Bayesian Capire il mondo con la probabilità

Introduzione al Teorema di Bayes

Il teorema di Bayes è un’idea potente e versatile utilizzata per aggiornare la nostra comprensione del mondo in base a nuove informazioni. È come una ricetta per combinare le nostre credenze precedenti con nuove prove per ottenere una visione più precisa della realtà. In poche parole, ci aiuta a capire quanto è probabile che qualcosa sia vero, dato quello che già sappiamo.

Il teorema di Bayes è come un detective che cerca di risolvere un caso. Inizia con un’idea iniziale su cosa potrebbe essere successo (la probabilità a priori) e poi usa nuove prove per aggiornare la sua idea (la probabilità a posteriori). Più prove ha, più precisa diventa la sua conclusione.

Esempi di applicazione del teorema di Bayes nella vita quotidiana

Il teorema di Bayes è ovunque, anche se non ce ne accorgiamo! Ecco alcuni esempi di come viene utilizzato nella vita quotidiana:

• Diagnosticare una malattia: I medici usano il teorema di Bayes per determinare la probabilità che un paziente abbia una certa malattia, in base ai sintomi che presenta.
• Filtrare lo spam: I filtri antispam utilizzano il teorema di Bayes per identificare le email indesiderate. Analizzano le parole e le frasi in un’email per determinare la probabilità che sia spam.
• Prevedere il tempo: I meteorologi utilizzano il teorema di Bayes per prevedere il tempo, combinando le previsioni dei modelli meteorologici con le osservazioni locali.
• Valutare il rischio: Le compagnie di assicurazione utilizzano il teorema di Bayes per valutare il rischio di un individuo, in base alla sua storia e alle sue caratteristiche.

Importanza del teorema di Bayes nell’inferenza statistica

Il teorema di Bayes è fondamentale nell’inferenza statistica, che è il processo di estrapolare conclusioni dai dati. È il fondamento di molti metodi statistici, tra cui:

• Modellazione bayesiana: Un approccio alla modellazione statistica che utilizza il teorema di Bayes per aggiornare le nostre credenze sui parametri di un modello, in base ai dati osservati.
• Test di ipotesi bayesiano: Un metodo per testare le ipotesi statistiche utilizzando il teorema di Bayes per calcolare la probabilità di un’ipotesi, dato i dati osservati.
• Stima bayesiana: Un metodo per stimare i parametri di un modello utilizzando il teorema di Bayes per ottenere la distribuzione di probabilità dei parametri, dato i dati osservati.

Il teorema di Bayes è un potente strumento per l’analisi dei dati e la presa di decisioni. Ci aiuta a capire il mondo che ci circonda in modo più preciso e a fare scelte più informate.

Applicazioni del Teorema di Bayes: Bayesian

Il Teorema di Bayes è uno strumento potente che può essere applicato in una vasta gamma di campi, dalla medicina all’ingegneria, dalla finanza alla scienza dei dati. In sostanza, il teorema ci aiuta a aggiornare le nostre credenze sulla probabilità di un evento in base a nuove informazioni.

Esempi di Applicazione del Teorema di Bayes

Il teorema di Bayes è utilizzato in diversi settori per prendere decisioni informate e risolvere problemi complessi. Di seguito sono riportati alcuni esempi specifici:

Medicina

In medicina, il teorema di Bayes viene utilizzato per diagnosticare le malattie. Ad esempio, un medico può utilizzare il teorema per calcolare la probabilità che un paziente abbia una particolare malattia, dato che ha presentato determinati sintomi.

Ingegneria

Nell’ingegneria, il teorema di Bayes viene utilizzato per progettare sistemi affidabili. Ad esempio, gli ingegneri possono utilizzare il teorema per calcolare la probabilità che un componente di un sistema si guasti, dato che ha già subito un certo numero di cicli di stress.

Finanza

In finanza, il teorema di Bayes viene utilizzato per valutare i rischi e gestire i portafogli. Ad esempio, gli analisti finanziari possono utilizzare il teorema per calcolare la probabilità che un investimento abbia successo, dato che il mercato sta attraversando un periodo di volatilità.

Scienza dei Dati

Nella scienza dei dati, il teorema di Bayes viene utilizzato per classificare i dati e costruire modelli predittivi. Ad esempio, gli scienziati dei dati possono utilizzare il teorema per classificare le e-mail come spam o non spam, in base al contenuto del messaggio.

Tabella di Esempi di Applicazione

La seguente tabella fornisce esempi specifici di come il teorema di Bayes viene utilizzato in diversi settori:

| Settore | Esempio |
|—|—|
| Medicina | Calcolo della probabilità di un paziente di avere una particolare malattia, dato che ha presentato determinati sintomi. |
| Ingegneria | Calcolo della probabilità che un componente di un sistema si guasti, dato che ha già subito un certo numero di cicli di stress. |
| Finanza | Calcolo della probabilità che un investimento abbia successo, dato che il mercato sta attraversando un periodo di volatilità. |
| Scienza dei Dati | Classificazione delle e-mail come spam o non spam, in base al contenuto del messaggio. |

Vantaggi e Svantaggi

L’utilizzo del teorema di Bayes presenta alcuni vantaggi e svantaggi:

Vantaggi

• Il teorema di Bayes è un approccio logico e matematico per aggiornare le nostre credenze sulla probabilità di un evento in base a nuove informazioni.
• Può essere utilizzato per prendere decisioni informate in situazioni di incertezza.
• È un approccio flessibile che può essere applicato a una vasta gamma di problemi.

Svantaggi

• Il teorema di Bayes può essere complesso da applicare, soprattutto per problemi con un gran numero di variabili.
• La precisione dei risultati dipende dalla qualità delle informazioni utilizzate.
• Può essere difficile ottenere dati accurati e completi per alcune applicazioni.

Approfondimenti sul Teorema di Bayes

Il Teorema di Bayes è uno strumento potente per aggiornare le nostre credenze alla luce di nuove informazioni. Per comprendere appieno questo teorema, è necessario approfondire i concetti chiave che lo compongono: probabilità a priori, probabilità a posteriori e probabilità condizionata.

Probabilità a priori, a posteriori e condizionata

La probabilità a priori rappresenta la nostra credenza iniziale sulla probabilità di un evento prima di osservare nuove informazioni. Ad esempio, la probabilità a priori di un dado che esca 6 è 1/6, basandoci sulla nostra conoscenza del dado.

La probabilità a posteriori, invece, rappresenta la nostra credenza aggiornata sulla probabilità di un evento dopo aver osservato nuove informazioni. Ad esempio, se lanciamo il dado 10 volte e otteniamo 6 cinque volte, la nostra probabilità a posteriori che esca 6 sarebbe maggiore di 1/6.

La probabilità condizionata, infine, rappresenta la probabilità di un evento dato che un altro evento si è già verificato. Ad esempio, la probabilità condizionata di ottenere 6 dato che il dado è stato lanciato e ha mostrato un numero pari è 1/3.

Calcolo della probabilità a posteriori

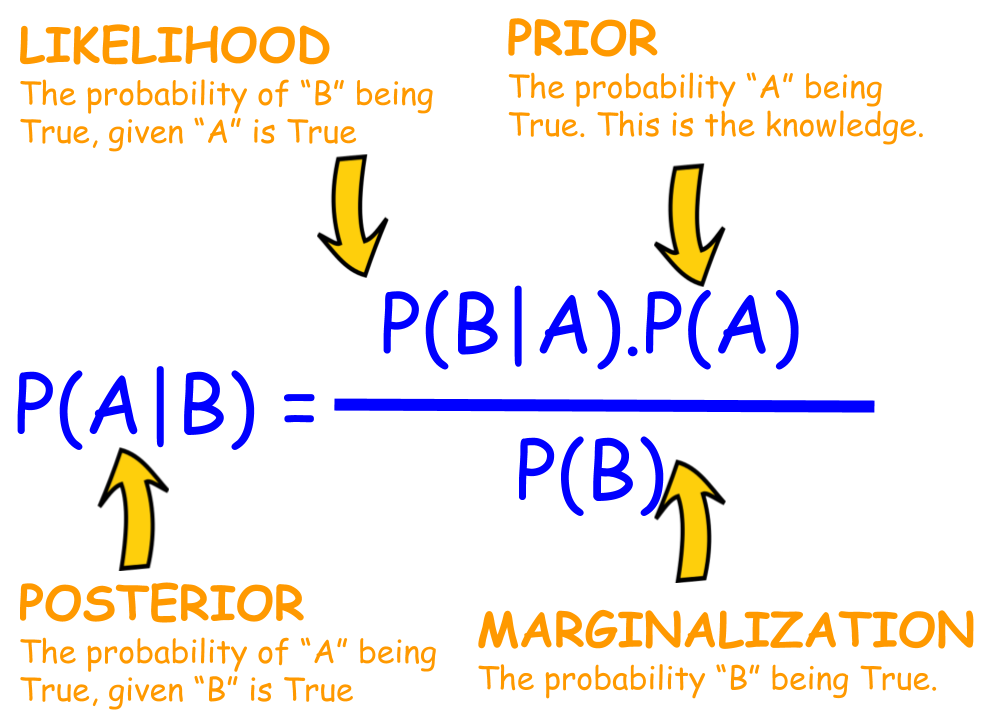
Il Teorema di Bayes fornisce una formula per calcolare la probabilità a posteriori di un evento:

P(A|B) = [P(B|A) * P(A)] / P(B)

Dove:

* P(A|B) è la probabilità a posteriori di A dato B.
* P(B|A) è la probabilità condizionata di B dato A.
* P(A) è la probabilità a priori di A.
* P(B) è la probabilità a priori di B.

Ad esempio, se vogliamo calcolare la probabilità che un paziente abbia una certa malattia (A) dato che il test è positivo (B), possiamo usare il Teorema di Bayes.

Interpretazioni e implicazioni filosofiche, Bayesian

Il Teorema di Bayes ha diverse interpretazioni e implicazioni filosofiche. Un’interpretazione comune è che il teorema rappresenta un modo per aggiornare le nostre credenze in modo razionale alla luce di nuove informazioni. Questa interpretazione ha implicazioni per la filosofia della scienza, poiché suggerisce che le teorie scientifiche dovrebbero essere aggiornate sulla base di nuove evidenze.

Un’altra interpretazione del Teorema di Bayes è che esso rappresenta un modo per calcolare la probabilità di un evento basato sulla sua probabilità condizionata. Questa interpretazione ha implicazioni per la teoria della probabilità, poiché suggerisce che la probabilità di un evento può essere calcolata in base alla probabilità di altri eventi che sono correlati ad esso.

Il Teorema di Bayes è uno strumento potente per la comprensione della probabilità e l’aggiornamento delle nostre credenze alla luce di nuove informazioni. Ha implicazioni importanti per la filosofia della scienza, la teoria della probabilità e altre discipline.

Bayesian statistics, a powerful tool for analyzing data, often relies on prior knowledge to inform its calculations. This is similar to how a successful entrepreneur like Mike Lynch, known for his luxurious yacht, the Lusso e Successo , might use past experiences to guide future investments.

Ultimately, Bayesian methods aim to refine our understanding of the world, just as a skilled entrepreneur like Lynch uses his insights to navigate the complexities of the business world.

Bayesian statistics is a powerful tool for making inferences about the world based on data. It allows us to update our beliefs about a hypothesis as we gather more evidence. This approach is particularly useful when dealing with uncertainty, as it provides a framework for incorporating prior knowledge into our analysis.

For a deeper dive into the world of Bayesian statistics, check out this article: bayesian. Bayesian methods are increasingly being used in fields like machine learning, healthcare, and finance, and they are likely to continue playing a significant role in our understanding of complex systems.